Ne è passato di tempo! Ma se siete qui, pronti per la seconda parte, vuol dire che non vi siete persi! Approfondiremo in questa seconda puntata il discorso dell’azimuth e parleremo di come stimare le distanze in mappa, per ora tutto senza ACE. Ma andiamo per ordine (dopo aver dato, magari, una bella ripassata):
Azimuth “diretto” e azimuth inverso o reciproco (“back azimuth”): di che parliamo?
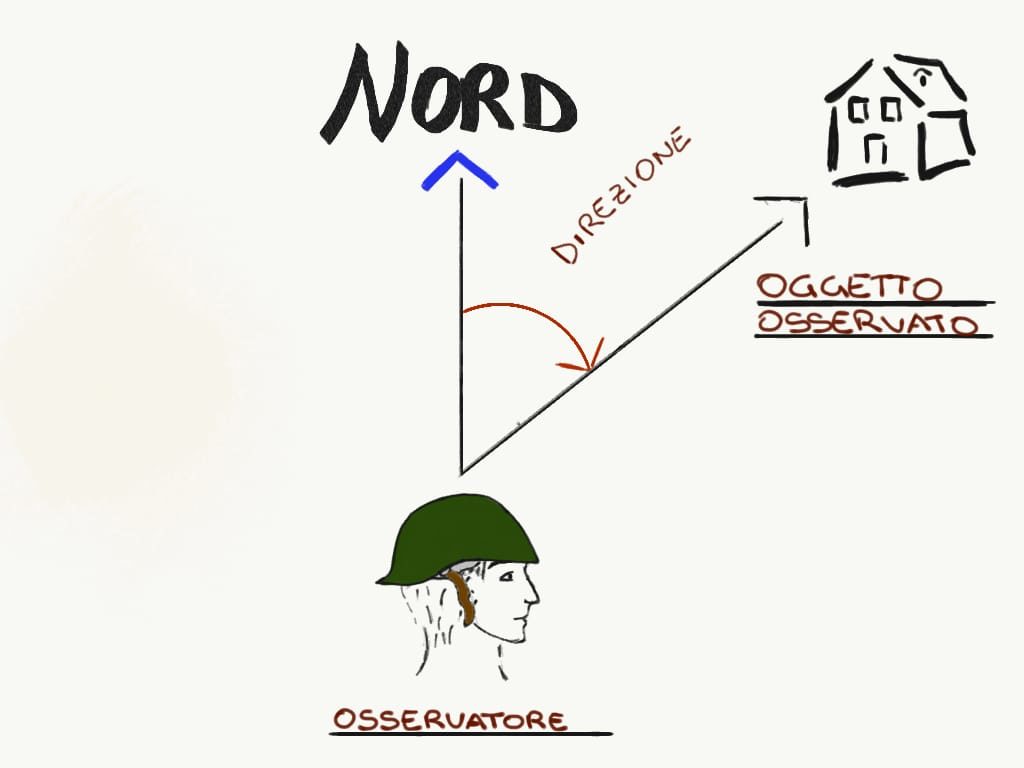
Familiarizzando con la bussola, abbiamo imparato a ricavare la direzione (o bearing, o azimuth che potremmo dire “diretto”) a partire da noi verso qualunque altra cosa. Abbiamo anche detto che non è altro che una distanza angolare dal Nord. Questa, ripetiamo, è la direzione a partire da noi verso un certo oggetto. Se dico che una casa è a gradi 105 da me, è evidente che il riferimento da cui parte la misurazione sono io. Dal punto di vista dell’oggetto osservato, io in che direzione mi trovo?
Azimuth inverso: in teoria…
Si sarebbe tentati di dire la stessa, e sarebbe così se parlassimo di una distanza metrica. Immaginiamo però di avere due persone, A e B, poste una davanti all’altra, faccia a faccia. La destra di A equivale alla sinistra di B, e viceversa. La cosa non è casuale: se io sono B, se so che qualcosa è a destra di A, dovrò guardare alla mia sinistra, e viceversa: sempre all’opposto – questa è la relazione – rispetto ad A.

Con gli azimuth la cosa è speculare: posso vedere dalla bussola in che direzione sia qualcosa rispetto a me, ma può anche servirmi sapere in che direzione sia io rispetto a questo qualcosa. È questo l’azimuth inverso (o opposto), legato ad una relazione geometrica abbastanza semplice. Perché quando una macchina da corsa fa un testacoda si dice che ha fatto un centottanta? Perché data una distanza angolare invertirla significa sempre aggiungere un’ampiezza di 180°. Non a caso 180° è la metà di 360°: se noi guardiamo in avanti e ci viene detto di girarci di 180°, dobbiamo voltarci alle nostre spalle. Altri 180° e torniamo nella direzione opposta, al punto di partenza. Insomma, se la casa è a 105° da me, io sono a 285° (cioè 105°+180°) dalla casa.
Noi misuriamo gli angoli solitamente in gradi sessagesimali, che vanno da 0° a 360°. Misure maggiori di 360 sono sempre possibili, ma un angolo maggiore di 360° coincide sempre con quello stesso angolo meno 360°. Un angolo di 450° coincide con un angolo di 90° (cioè 450°-360°), ad esempio, e 360° coincide con 0°, cioè 360°-360°.
…e in pratica…
Sperando che chi odia la geometria non sia scappato a gambe levate (o corso ad armarsi), diamo quindi la regoletta.

Noto l’azimuth da A verso B (azimuth diretto), l’azimuth da B verso A (azimuth inverso) è dato 1) da azimuth diretto + 180° se l’azimuth diretto è minore o uguale a 180°; 2) da azimuth diretto – 180° se l’azimuth diretto è maggiore di 180°.
Invertire una direzione non significa sempre aggiungere 180°? Certamente, ma nel caso di un angolo maggiore di 180° l’addizione significherebbe arrivare ad un angolo maggiore di 360°; con la regoletta, si sottrae per fare un calcolo in meno (senza aggiungere 180° e dover togliere 360°).
Se abbiamo una bussola, possiamo ricordare la regoletta guardando il quadrante. Basta sfruttare i punti cardinali: so che Nord equivale a 0° e il suo opposto è il Sud, guarda caso a 180°! So che Est equivale a 90° e il suo opposto è l’Ovest, a 270° (=90°+180°). Ovviamente il discorso si può fare all’inverso (è il caso di dirlo…): l’opposto di 270° (valore maggiore di 180°) è 90°, cioè 270°-180°, e così via. Attenzione a non sbagliare i calcoli!
… ma perché?
A questo punto si può pensare: Bell’excursus trigonometrico (e chi pensa che la trigonometria non serva in ambito militare, faccia “amicizia” con cecchini o artiglieri…), ma a che serve? Consideriamo tre casi (per ora ignorando le distanze metriche).
1) Sto seguendo una certa direzione (o disegnando una rotta in mappa); a un certo punto devo seguire (o disegnare) la direzione esattamente opposta. Questa non è altro che l’azimuth inverso della direzione originaria.

2) Pianificando una rotta, devo aggirare un ostacolo naturale (o un’area pericolosa o nemica). Per farlo dovrò pianificare diversi cambi di direzione, andando varie volte in direzione opposta ad una precedente. Di volta in volta, questa direzione opposta non è altro che un azimuth inverso. L’esempio di destra usa, per semplificare, i punti cardinali, ma sul campo le direzioni potranno essere le più varie (ecco perché è importante fare i calcoli giusti!).
3) Mi sono perso, ma trovo un punto di riferimento (ad esempio un faro) identificabile in mappa. Riesco a stimare che dista da me 500 metri ed è a 140° dalla mia posizione. Se il faro è a 140° da me, io sono a 320° da lui (l’azimuth inverso di 140° = 140°+180° perché 140° < 180°). Se dal faro in mappa traccio una linea lunga 500 metri (introdurremo il discorso delle distanze a breve) in direzione 320°, questa linea finirà proprio nel punto in cui mi trovo. Per triangolare la propria posizione a partire da riferimenti in mappa la situazione è simile.
Distanze in mappa
Una carta topografica è una rappresentazione simbolica (e non una fotografia) di una certa realtà fisica che dal vero è assai più grande. Per ovvie ragioni di spazio, le distanze reali (a meno che non si tratti di realtà poco estese, come una stanza) non sono riprodotte uno a uno, ma in scala (come il modellino di un aereo, ma in 2D invece che in 3D). La griglia che incasella la mappa in ArmA e che rispetta la scala ci permette di stimare le distanze quasi senza calcoli.
Diciamolo subito: le distanze misurate in mappa sono sempre distanze in linea d’aria: distanze “in 2D“. Queste corrispondono alle distanze reali sul terreno solo in assenza completa di rilievi (in un contesto “piatto”: il mare, una pista d’atterraggio, eccetera). Salite e discese (il mondo “3D”), come impareremo e come sanno bene i cecchini “in quota”, influiscono sulle distanze reali.
Quadrati…
Abbiamo imparato a ricavare dalla fidata griglia della mappa le coordinate chilometriche. Il nome, che rimanda al termine chilometro, fa sospettare che queste coordinate abbiano a che vedere con le distanze, ed è proprio così. Prendiamo una sezione di Stratis:
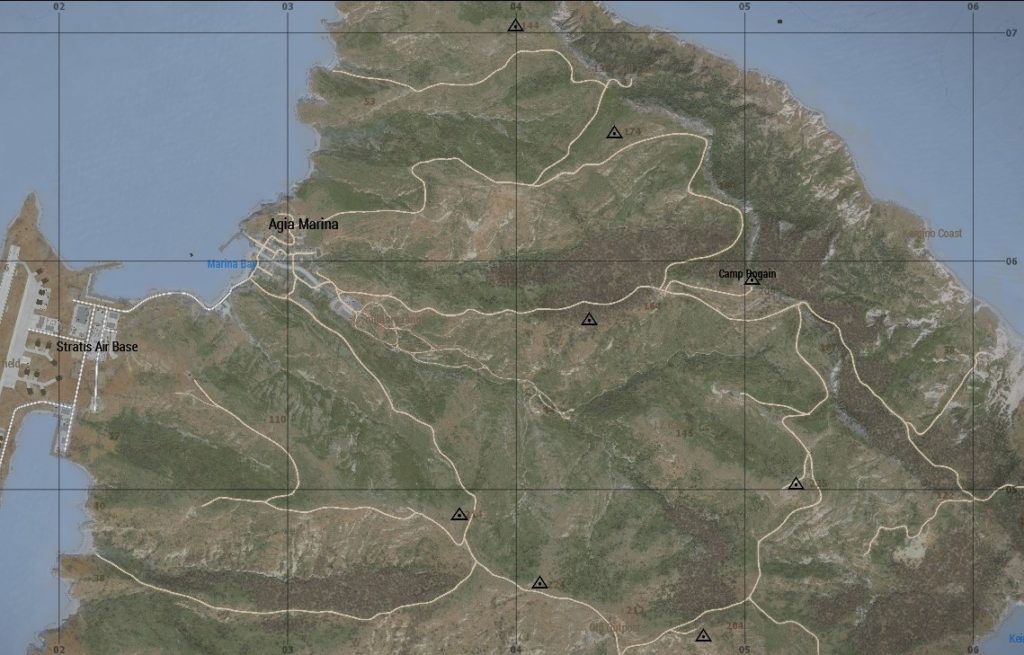
Notiamo in alto che, a questo livello di zoom, sono mostrate le coordinate a due cifre. Vediamo dei quadrati tutti uguali: ogni lato misura esattamente 1 km (= 1000 m), e ogni quadrato rappresenta un’area di 1 km² (= 100 ettari). Ogni cifra di una coordinata ha un significato metrico. In un’ipotetica coordinata 12, la prima cifra indica le decine di chilometri (qui 1×10 km = 10 km), la seconda indica i chilometri (qui 2×1 km = 2 km). Tutte queste distanze partono, in orizzontale e verticale, da un’origine 000 opportunamente scelta: disegnandole via via, si costruisce il reticolato in mappa. Noi per il momento vediamo due cifre (decine di chilometri e chilometri) e l’unità di riferimento è data sempre dall’ultima cifra che vediamo, il chilometro, in questo caso. E se zoomiamo?
…e quadratini
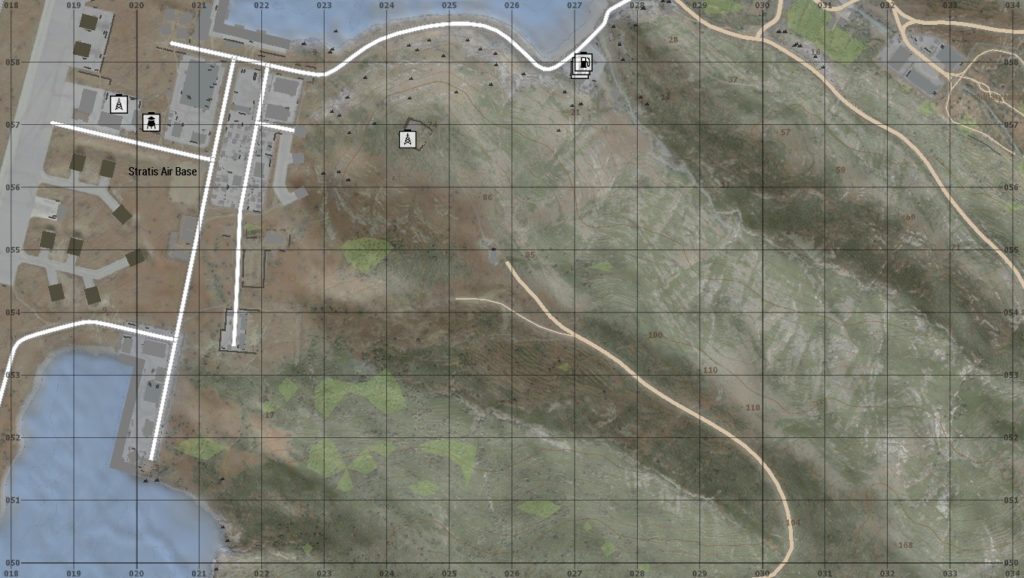
Ecco che vediamo le coordinate a tre cifre. La mappa è più precisa, e così anche le distanze. Nel solo quadrato che avevamo prima si inseriscono dieci quadratini più piccoli e tutti uguali: ogni lato di questi quadratini misura esattamente 100 m (=1/10 di km), ogni quadratino ha area di 10000 m², cioè 0,01 km² = 1 ettaro . In una coordinata a tre cifre come 123, infatti, le prime due cifre indicano quel che abbiamo detto, la terza cifra indica i decimi di chilometro (e, poiché 1 km = 1000 m, 1/10 di km = 100 m). L’unità di riferimento è data sempre dall’ultima cifra, quindi in questo caso abbiamo le centinaia di metri.
Cominciamo a “prendere le distanze”…
Per “spiccare il volo” con le distanze in mappa, perché non misurare una pista d’atterraggio? Lo so, questa era pessima…
Dalla mappa, con lo zoom tale da avere come unità di misura il chilometro (visualizziamo infatti le coordinate a due cifre), notiamo che, con una prima approssimazione, la pista è lunga all’incirca come il lato del quadrato, lungo un chilometro.
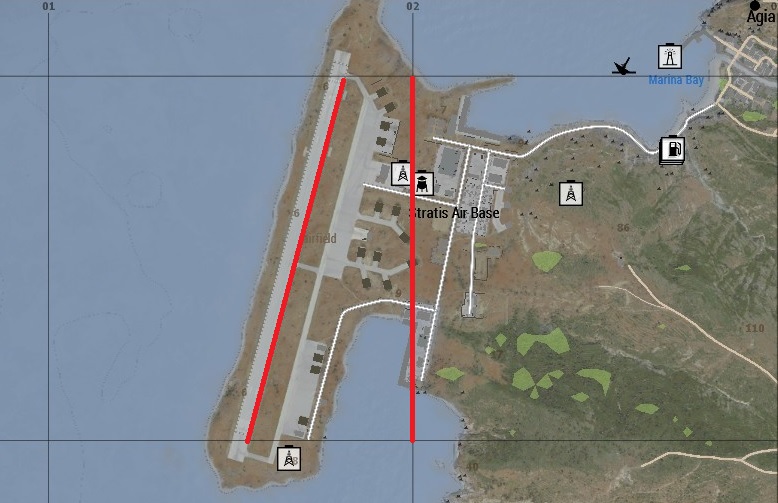
Se vogliamo essere più precisi (ma sempre con un grado di approssimazione), zoomiamo fino ad avere le coordinate a tre cifre visibili e, quindi, le centinaia di metri come unità.

Ogni quadratino ha lato pari a 100 m. Se contiamo i quadratini (magari visualizzando o tracciando una linea lungo il profilo della pista) e moltiplichiamo il numero dei quadratini per 100 m, avremo una stima migliore della distanza che, in questo caso, rappresenta la lunghezza della pista.
Contiamo 12 quadratini. 12×100 m = 1200 m (= 1,2 km). Misurando, tramite comandi script del gioco, l’effettiva distanza tra i due punti neri qui visibili, questa risulta di 1164 metri. Lo scostamento è stato quindi di 36 metri, non male per una stima fatta con un rapido conteggio e una facile moltiplicazione per 10.
Diagonali
Si può dimostrare (col teorema di Pitagora) che la diagonale di un quadrato di lato l è data da l x √2, in cui approssimeremo √2 a 1,41. Coi quadrati di 1 km di lato, dunque, la diagonale misurerà 1 km x 1,41 = 1,41 km o 1410 m; coi quadrati di 100 m di lato, la diagonale misurerà 100 m x 1,41 = 141 m (= 0,14 km).
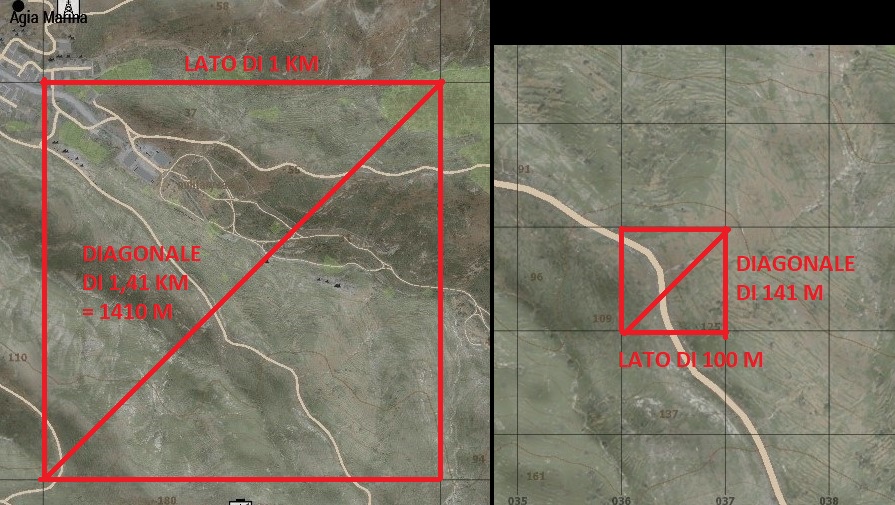

Ovviamente sarà molto comodo, in certi casi, considerare quadrati “combinati” di lato che è multiplo dell’unità, in genere multiplo di 100 m. In questo caso la moltiplicazione può essere meno rapida da fare a mente. Un rapido esempio: se abbiamo un quadrato il cui lato è dato dalla misura di due quadratini (100 m + 100 m), la diagonale sarà di 200 m x 1,41, ovvero 282 m.
Un altro esempio
Poniamo di essere nel verde della bella Stratis, al marker “Punto di partenza”, e di voler sapere quanto disti dalla nostra posizione il “Punto di arrivo” più a Nord Est da noi. La distanza più breve (in linea d’aria…) tra due punti è una retta passante per i due punti, no?

Ecco, guarda caso, la nostra diagonale, diagonale di un quadratone di lato 300 m (ho evidenziato in blu due dei quattro lati per migliore leggibilità). Avrete capito dove voglio arrivare: la distanza in questione è data da 300 m x 1,41 = 423 m. Contando i quadratini, avremmo stimato 300 m, che non è troppo male (tralasciando ora gli aspetti relativi a dislivelli vari). Secondo i comandi script, la distanza “2D” reale è di 424 m.
Lo stesso punto si può raggiungere anche in altri modi: se ne preferirà in base a ragioni di percorribilità o all’opportunità di evitare ostacoli o pericoli, ma per ora non approfondiamo. Diamo invece un’altra proposta:
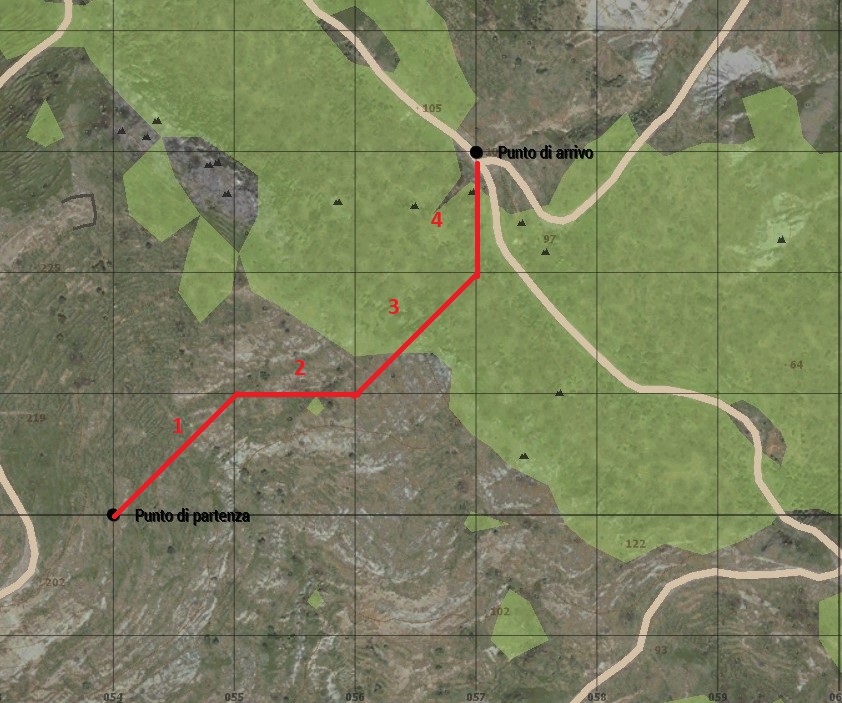
Qui abbiamo una bella situazione mista. In due casi (quadratini 2 e 4), ci muoviamo direttamente sul lato del quadratino (ma potrebbe anche essere una parallela al lato, nulla cambierebbe) ; nei quadratini 1 e 3 il movimento segue la diagonale. Facciamo gli ultimi conti della puntata:
Una diagonale equivale a 100 m x 1,41 = 141 m, e quindi il movimento su due diagonali equivale a 141 m x 2 = 282 m. Come ormai sappiamo bene, muovendoci sul lato percorriamo invece 100 m, e, facendolo due volte, 200 m. Il percorso totale è così di 482 m. Più lungo della via più breve, è ovvio, ma ricordiamoci che parliamo di distanze in linea d’aria. La realtà 3D del terreno, che impareremo a leggere dalla carta, può cambiare le cose. E il terreno comanda. Ma con queste preziose, spero, nozioni riuscirete più facilmente a farci i conti (anche qui, è il caso di dirlo…)
Alla prossima e buon orienteering!










